•Loop amplitude

Construction of topologies:

tops = CreateTopologies[1, 1 -> 1, Adjacencies -> {3}, CountertermOrder -> 0, ExcludeTopologies -> Tadpoles] ;

Fields insertion:

inserttops = InsertFields[tops, {Electron[0]} -> {Electron[0]}, Model -> "Automatic", GenericModel -> "Automatic", InsertionLevel -> Classes] ;

Graphical representation of the process:

Paint[inserttops, PaintLevel -> {Classes}, AutoEdit -> False, SheetHeader -> False, Numbering -> False, ColumnsXRows -> 1] ;

[Graphics:../HTMLFiles/index_60.gif]

Calculation of the amplitude:

amplFC = CreateFCAmp[inserttops, DiracTraceEvaluate -> True][[1]] /. ParticleMass[Photon, ___] -> 0 /. p3 -> -p1 // Simplify

(i ϕ ( p _ 1 , m _ ψ^(ó  0 ) ) . (e^(0 ) γ^μ _ 2) . (γ · q _ 1 + m _ ψ^(ó  0 )) . (e^(0 ) γ^μ _ 1) . ϕ ( p _ 1 , m _ ψ^(ó  0 ) ) g^(μ _ 1 μ _ 2))/(16 π^4 (q _ 1^2 - (m _ ψ^(ó  0 ))^2) . (q _ 1 - p _ 1)^2)

The one-loop integrals are simplified, the spinors are divided off:

aff = OneLoopSimplify[amplFC, q1, Dimension -> D] // DiracSimplify // Simplify

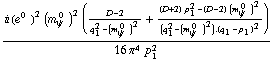
(i (e^(0 ))^2 (m _ ψ^(ó  0 ))^2 ((D - 2)/(q _ 1^2 - (m _ ψ^(ó  0 ))^2) + ((D + 2) p _ 1^2 - (D - 2) (m _ ψ^(ó  0 ))^2)/(q _ 1^2 - (m _ ψ^(ó  0 ))^2) . (q _ 1 - p _ 1)^2))/(16 π^4 p _ 1^2)

The loop integrals are expressed in terms of Passarino-Veltman symbols:

ampreduced = FullSimplify /@ Collect[OneLoop[q1, aff], _B0]

((e^(0 ))^2 (p _ 1^2 - A _ 0 ( (m _ ψ^(ó  0 ))^2 )) (m _ ψ^(ó  0 ))^2)/(8 π^2 p _ 1^2) + (B _ 0 (p _ 1^2, 0, (m _ ψ^(ó  0 ))^2) (e^(0 ))^2 ((m _ ψ^(ó  0 ))^2 - 3 p _ 1^2) (m _ ψ^(ó  0 ))^2)/(8 π^2 p _ 1^2)

The Passarino-Veltman integrals are evaluated:

ampinfinitiesfull = VeltmanExpand[ampreduced, B0Evaluation -> "direct1", ExpandGammas -> False, DimensionExpand -> False, SmallEpsilon -> 0] // FullSimplify

1/(8 π^4 p _ 1^2) (μ^(-D) (e^(0 ))^2 ((m _ ψ^(ó  0 ))^2 (π^2 (p _ 1^2 - (m _ ψ^(ó  0 ))^2) μ^D + π^(D/2) Γ(2 - D/2) (Underoverscript[∫, 0, arg3] ((x - 1) (x p _ 1^2 - (m _ ψ^(ó  0 ))^2))^(D - 4)/2 d x) ((m _ ψ^(ó  0 ))^2 - 3 p _ 1^2) μ^4) - π^(D/2) μ^4 Γ(2 - D/2) ((m _ ψ^(ó  0 ))^2)^(D/2)))

The value of the integral at p _ 1^2= m _ ψ^2, which for this expression is equivlent to γ p _ 1= m _ ψ:

sigmafullOnShell = Limit[(ampinfinitiesfull // ExpandGammas[#, TaylorOrder -> 2] & // DimensionExpand[#, TaylorOrder -> 1, Dimension -> D] &) /. Pair[Momentum[p1], Momentum[p1]] -> ParticleMass[Electron, RenormalizationState[0]]^2 + δ /. IntegrateHeld -> Integrate, δ -> 0] // Simplify

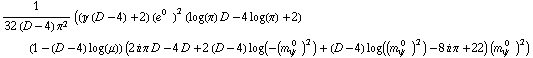
1/(32 (D - 4) π^2) ((÷J (D - 4) + 2) (e^(0 ))^2 (log(π) D - 4 log(π) + 2) (1 - (D - 4) log(μ)) (2 i π D - 4 D + 2 (D - 4) log(-(m _ ψ^(ó  0 ))^2) + (D - 4) log((m _ ψ^(ó  0 ))^2) - 8 i π + 22) (m _ ψ^(ó  0 ))^2)

Converted by Mathematica  (July 10, 2003)