•Renormalization

The counterterm amplitude:

lala = ArgumentsSupply[Lagrangian[QED[2]], x, RenormalizationState[0]]

-δm^(0 ) Z _ 2^(0 ) Overscript[ψ^(0 ), _] . ψ^(0 ) - 1/4 (Z _ 3^(0 ) - 1) (∂ _ μ A^(0 ) _ ν^ó  - ∂ _ ν A^(0 ) _ μ^ó ) . (∂ _ μ A^(0 ) _ ν^ó  - ∂ _ ν A^(0 ) _ μ^ó ) + (Z _ 2^(0 ) - 1) (Overscript[ψ^(0 ), _] . γ^μ . (e^(0 ) A^(0 ) _ μ . ψ^(0 ) + i ∂ _ μ ψ^(0 ) _ ó ^ó ) - Overscript[ψ^(0 ), _] . ψ^(0 ) m _ ψ^(ó  0 ))

amp4 = -I FeynRule[lala, {QuantumField[Particle[Vector[1], RenormalizationState[0]], LorentzIndex[μ1]][p2], QuantumField[Particle[Vector[1], RenormalizationState[0]], LorentzIndex[μ2]][p1]}] /. p2 -> -p1 // Simplify

(Z _ 3^(0 ) - 1) (p _ 1^μ _ 1 p _ 1^μ _ 2 - g^(μ _ 1 μ _ 2) p _ 1^2)

piintegral = (ampinfinitiesfull + amp4)/tensor // Cancel // Simplify

1/(36 π^4 p _ 1^2 (m _ ψ^(ó  0 ))^2) (μ^(-D) (-6 π^(D/2) (e^(0 ))^2 Γ(2 - D/2) (((m _ ψ^(ó  0 ))^2)^(D/2) - (Underoverscript[∫, 0, arg3] ((m _ ψ^(ó  0 ))^2 + (x - 1) x p _ 1^2)^(D - 4)/2 d x) (m _ ψ^(ó  0 ))^4) μ^4 - (36 π^4 (Z _ 3^(0 ) - 1) μ^D + (e^(0 ))^2 (π^2 μ^D - 3 π^(D/2) μ^4 Γ(2 - D/2) Underoverscript[∫, 0, arg3] ((m _ ψ^(ó  0 ))^2 + (x - 1) x p _ 1^2)^(D - 4)/2 d x)) p _ 1^2 (m _ ψ^(ó  0 ))^2))

We now add the two amplitudes and demand that the momentum coefficients of this sum vanish at p _ 1^2= 0.  This demand is equivalent to demanding that the complete photon propagator have the same pole position and residue as the bare propagator apart from gauge dependent terms (see e.g. Weinberg).

piintegral0 = pi0full + amp4/tensor // Cancel // Simplify ;

This is then the value of Z _ 3 (infinite in the limit D->4) following from this demand:

z3solve = Solve[(piintegral0) == 0, CouplingConstant[QED[2], 3, RenormalizationState[0]]] // Flatten // Simplify

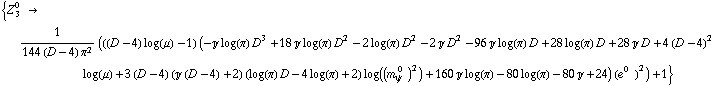
{Z _ 3^(0 ) -> 1/(144 (D - 4) π^2) (((D - 4) log(μ) - 1) (-÷J log(π) D^3 + 18 ÷J log(π) D^2 - 2 log(π) D^2 - 2 ÷J D^2 - 96 ÷J log(π) D + 28 log(π) D + 28 ÷J D + 4 (D - 4)^2 log(μ) + 3 (D - 4) (÷J (D - 4) + 2) (log(π) D - 4 log(π) + 2) log((m _ ψ^(ó  0 ))^2) + 160 ÷J log(π) - 80 log(π) - 80 ÷J + 24) (e^(0 ))^2) + 1}

The scalar integral with the above value of Z _ 3 inserted and the limit D->4 taken.  The result is finite:

piint = (piintegral /. z3solve) // ExpandGammas[#, TaylorOrder -> 2] & // DimensionExpand[#, TaylorOrder -> 1, Dimension -> D] & // Collect[#, _IntegrateHeld] & ;

plim = piint /. IntegrateHeld[a_, b__] /; FreeQ[a, Log] :> Integrate[a, b] /. D -> 4 - δ // Collect[#, _IntegrateHeld] & // Simplify ;

piren = Simplify /@ (Limit[plim, δ -> 0] // Collect[#, {_IntegrateHeld, _Log}] &)

-((Underoverscript[∫, 0, arg3] log((m _ ψ^(ó  0 ))^2 + (x - 1) x p _ 1^2) d x) (2 (m _ ψ^(ó  0 ))^2 + p _ 1^2) (e^(0 ))^2)/(12 π^2 p _ 1^2) + (log((m _ ψ^(ó  0 ))^2) (2 (m _ ψ^(ó  0 ))^2 + p _ 1^2) (e^(0 ))^2)/(12 π^2 p _ 1^2) - (e^(0 ))^2/(36 π^2)

We may evaluate the integral with some numeric value of the constants:

piren /. {_ParticleMass^2 -> 1, _Pair -> p2, _CouplingConstant -> 1} /. IntegrateHeld -> Integrate // FullSimplify

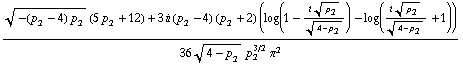
((-(p _ 2 - 4) p _ 2)^(1/2) (5 p _ 2 + 12) + 3 i (p _ 2 - 4) (p _ 2 + 2) (log(1 - (i p _ 2^(1/2))/(4 - p _ 2)^(1/2)) - log((i p _ 2^(1/2))/(4 - p _ 2)^(1/2) + 1)))/(36 (4 - p _ 2)^(1/2) p _ 2^(3/2) π^2)

The above is in agreement with the evaluation of the textbook formula (Weinberg equation 11.2.22):

piWeinberg = 1/(2 π^2) ((IntegrateHeld[(1 - x) x Log[1 - (1 - x) x Pair[Momentum[p1], Momentum[p1]]/ParticleMass[Fermion[7], RenormalizationState[0]]^2], {x, 0, 1}]) CouplingConstant[QED[1], RenormalizationState[0]]^2)

((e^(0 ))^2 Underoverscript[∫, 0, arg3] (1 - x) x log(1 - ((1 - x) x p _ 1^2)/(m _ ψ^(ó  0 ))^2) d x)/(2 π^2)

piWeinberg /. {_ParticleMass -> 1, _Pair -> p2, _CouplingConstant -> 1} /. IntegrateHeld -> Integrate // FullSimplify

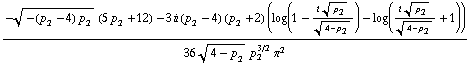
(-(-(p _ 2 - 4) p _ 2)^(1/2) (5 p _ 2 + 12) - 3 i (p _ 2 - 4) (p _ 2 + 2) (log(1 - (i p _ 2^(1/2))/(4 - p _ 2)^(1/2)) - log((i p _ 2^(1/2))/(4 - p _ 2)^(1/2) + 1)))/(36 (4 - p _ 2)^(1/2) p _ 2^(3/2) π^2)

Converted by Mathematica  (July 10, 2003)