![]()
These rules can be applied to fourth order expressions:
![]()
Simplify logs
![]()
We will work in the limit ![]() =
=![]() :
:
![]()
![]()
Translating from masses of isostates to particle states (no pi-eta mixing):
![subpar = Table[(ParticleMass[PseudoScalar[1], SUNIndex[i], r___] -> ParticleMass[Select[$IsoSpinProjectionRules, (! FreeQ[#, {i}] &)][[1]][[1]], r]), {i, 8}]](../HTMLFiles/index_17.gif)
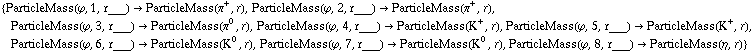
![WFFactor1[_[__, Scalar2[0, ___]]] := 0 ; WFFactor1[_[__, PseudoScalar0[0, ___]]] := 0 ; WFFactor1[Propagator[p_][v__, PseudoScalar1[0, {1}]]] := WFFactor[Propagator[p][v, PseudoScalar2[0]]] ; WFFactor1[Propagator[p_][v__, PseudoScalar1[0, {2}]]] := WFFactor[Propagator[p][v, PseudoScalar2[0]]] ; WFFactor1[Propagator[p_][v__, PseudoScalar1[0, {3}]]] := WFFactor[Propagator[p][v, PseudoScalar2[0]]] ; WFFactor1[Propagator[p_][v__, PseudoScalar1[0, {4}]]] := WFFactor[Propagator[p][v, PseudoScalar6[0]]] ; WFFactor1[Propagator[p_][v__, PseudoScalar1[0, {5}]]] := WFFactor[Propagator[p][v, PseudoScalar6[0]]] ; WFFactor1[Propagator[p_][v__, PseudoScalar1[0, {6}]]] := WFFactor[Propagator[p][v, PseudoScalar6[0]]] ; WFFactor1[Propagator[p_][v__, PseudoScalar1[0, {7}]]] := WFFactor[Propagator[p][v, PseudoScalar6[0]]] ; WFFactor1[Propagator[p_][v__, PseudoScalar1[0, {8}]]] := WFFactor[Propagator[p][v, PseudoScalar11[0]]] ;](../HTMLFiles/index_19.gif)
The Gell-Mann-Okubo mass formula (will be applied only on 4th order expressions):
![]()
![toEtaRules = {ParticleMass[PseudoScalar[2], r___]^2 - 4 ParticleMass[PseudoScalar[6], r___]^2 :> -3 * ParticleMass[PseudoScalar[11], r]^2, -ParticleMass[PseudoScalar[2], r___]^2 + 4 ParticleMass[PseudoScalar[6], r___]^2 :> 3 * ParticleMass[PseudoScalar[11], r]^2} ;](../HTMLFiles/index_21.gif)
NOTICE: The default convention of Phi is at variance with the default convention of FeynCalc w.r.t. Mandelstam variables (t<->u). Below u is correspondingly written before t, setting the FeynCalc Mandelstam variables in agreement with the Phi default convention. Uncommenting should speed things up a great deal.
![manrules = {-MandelstamS - MandelstamT :> MandelstamU - 4 ParticleMass[Kaon, RenormalizationState[1]]^2, MandelstamS + MandelstamT :> -MandelstamU + 4 ParticleMass[Kaon, RenormalizationState[1]]^2, a_ MandelstamS + a_ MandelstamT :> a (-MandelstamU + 4 ParticleMass[Kaon, RenormalizationState[1]]^2)}](../HTMLFiles/index_22.gif)
![]()
![]()
Converted by Mathematica (July 10, 2003)